This class is bifurcated into two different tiers. The basic tier is a general overview of the conceptual applications of optimization. The advanced tier will include all content in the first, plus some videos discussing the mathematical solution of optimization problems, as well as additional homework to apply the mathematical solution to some real-world problems.
If you’re comfortable with basic calculus and advanced algebra, then you should take the advanced course. Otherwise, sticking with the basic tier will get you ~80% of the insight of the advanced version.
Office Hours
If you have any basic conceptual confusion about how optimization works, DM me (@DESpear#1689) and ask for help.
Material
- Unconstrained Optimization (see section below)
Advanced
- Unconstrained Optimization Math Tutorial
- Constrained Optimization Math Tutorial Part 1
- Constrained Optimization Math Tutorial Part 2
Homework
- Think about an unconstrained optimization problem you’re facing in real life. If possible, tie it into a previous course.
Advanced
- For the optimization problem, come up with a reasonable utility function for the decision and solve it.
- For the bug hunting/squashing tradeoff, come up with a reasonable utility function with diminishing marginal utility in both activities, and a constraint function in terms of time, then solve it.
A quadratic function with a negative x^2 term will produce the correct shape. You might want to try picking three points with approximable utility and then deriving a fitting curve from them. For further guidance, see the lecture from Practical Decision-Making on deriving utility curves. For even further guidance, try to arrange office hours with me (@DESpear#1689).
Cohort
Discuss the homework with your cohort.
Unconstrained Optimization
Welcome to the first and only week of the Guild of the ROSE class, The Practical Uses of Optimization. I will be your instructor, David the Economic Model (@DESpear#1689).
This course focuses on a broad, literary understanding of the concepts of optimization, as well as their practical application in daily life.
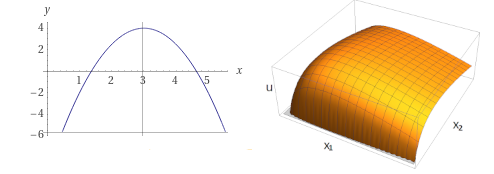
The two types of optimization we’ll be discussing are unconstrained, like the picture on the left, and constrained, like the picture on the right. As I’m sure you can imagine, constrained optimization problems is more mathematically and conceptually complex, but it’s also much more useful. If you’re taking the advanced version of the class, make sure you’re familiar with the math underlying these concepts before you watch the videos. If you’re taking the basic version, then I’ll occasionally make some asides for the mathy people. Don’t worry about them too much.
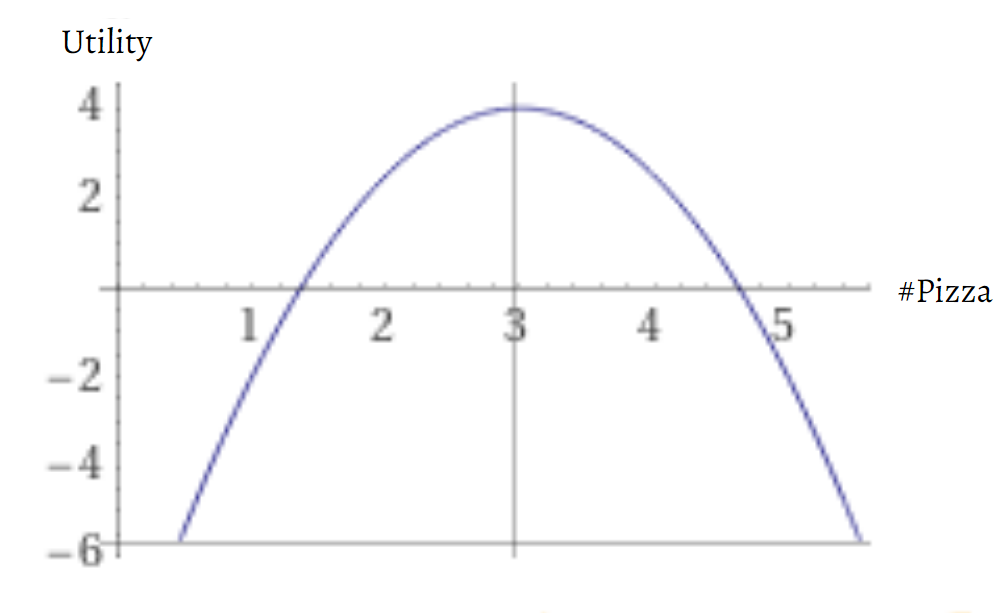
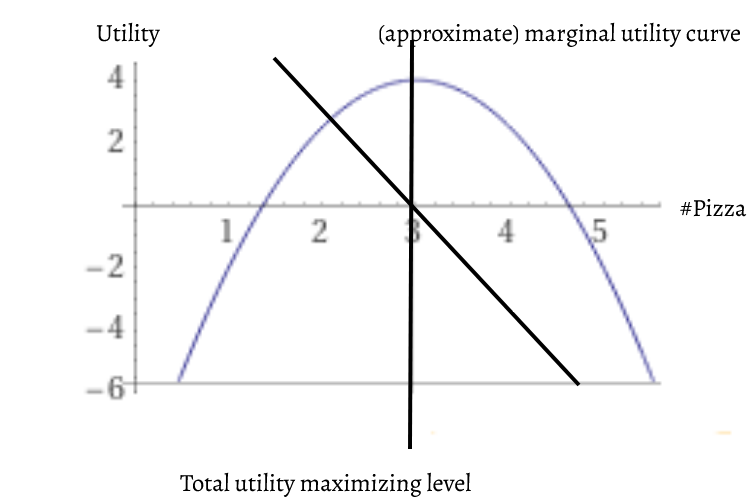
So, let's start with unconstrained optimization. Imagine that you’re going to an all-you-can-eat pizza buffet. Here we have a utility curve* showing the relationship between utility and pizza consumption. On the left part of the slope, your first few slices are wonderful. As we get to the top, things start leveling out. Then, over on the right, you start to get uncomfortably full. And then we get way over here to the level where you’re starting to worry about rupturing your stomach. So, we know that on the far left, there’s a low utility level of pizza where we’ve paid for the buffet but haven’t gotten our money’s worth, and on the far right there’s a low utility level where we land in the hospital.
Refer to Practical Decision-Making session 3 for help on plotting utility curves.
If you are facing a decision where both low and high values of something are low-utility and an intermediate value is higher then this is an unconstrained optimization problem
Now, just looking at the graph, it’s obvious what the optimal amount of pizza is. You can figure it out with a steady hand and straight edge. Or, if you’re taking the advanced course, you can find it exactly with the function which I used to derive this curve.
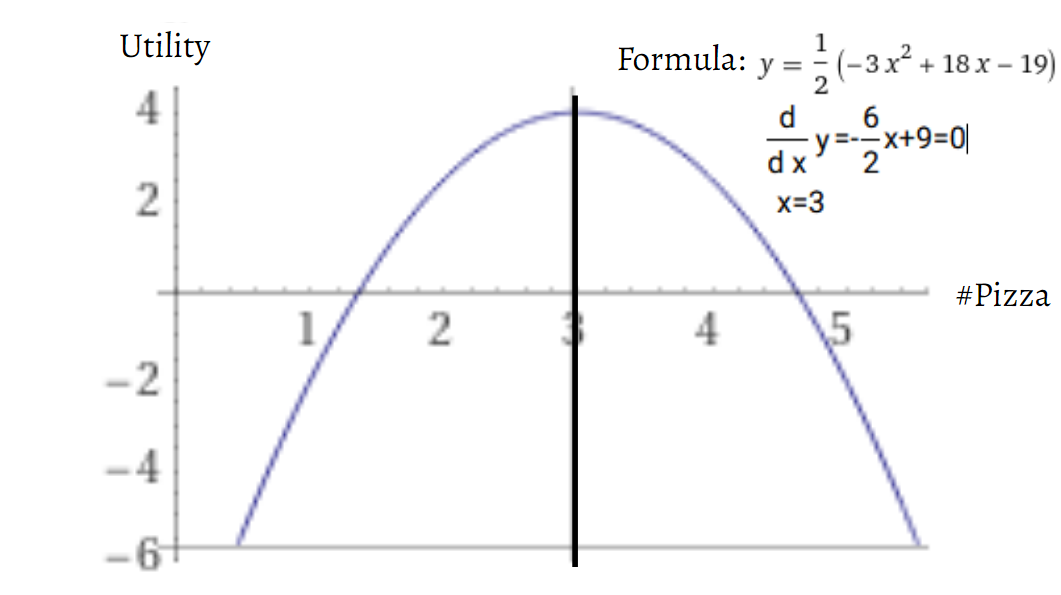
Take a minute to solve this optimization.
Okay, anyone who got 3 slices, well done. Everyone else, you can stay behind after class to clean the erasers.
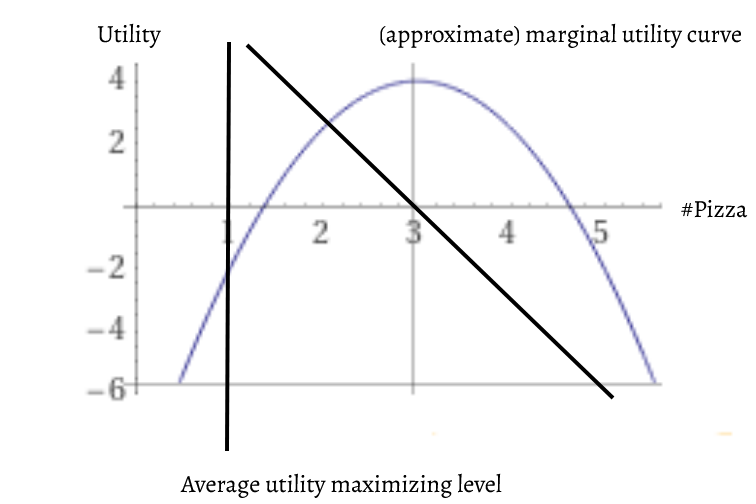
Now, there’s three more lessons we can learn about decision making from constrained optimization.
The first and most important is how to properly consider and use marginal utility. Marginal utility is essentially the concept of, for a given level of pizza, how much the next piece of pizza will satisfy you. To be even more precise, it’s how much the next miniscule bite will satisfy you. You can use the concept with discrete quantities like whole slices of pizza, but that significantly complicates the math without actually changing the underlying principle. If you really want to get into the weeds, the search term is “discrete optimization”. But for this course’s purposes, we’re just going to continue assuming a continuous function.
With that assumption in place, the advanced students probably recognize the marginal utility function as equal to the first derivative of the utility function with respect to the object of the decision.
Now, this is something where smart, mathy people who’ve never been directly exposed to utility analysis sometimes make mistakes. If you ask an engineer what the best number of floors to give an office building, they’ll sometimes give answers like “whatever maximizes the average profit” (vertically labeled “average maximization” appears at the “one slice” level) or something like that. In fact, it’s whatever number sets the marginal profit to zero.
If you are facing a decision where both low and high values of something are low-utility and an intermediate value is higher then this is an unconstrained optimization problem. And that’s our second lesson. When solving an unconstrained optimization, the solution is whatever sets the marginal utility to zero. In other words, you should start eating pizza until you expect the next bite will give you no net satisfaction, then stop.
The third and fourth lessons are that, when you’re dealing with an unconstrained optimization, getting the answer a little wrong is not a big deal (rule three appears on the slide), but that the marginal dropoff in utility will become bigger the farther from the optimum you are.
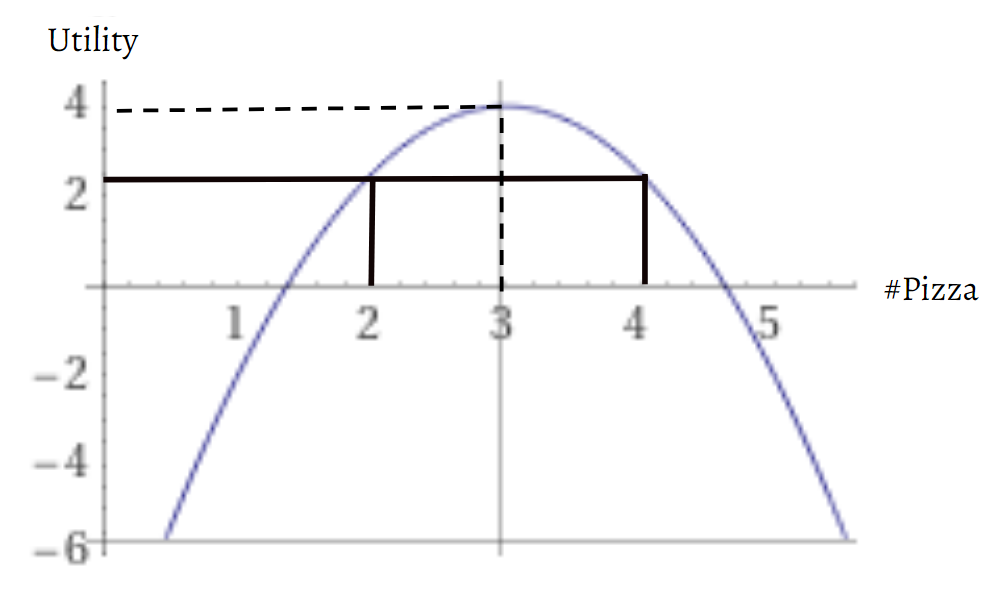
Notice that if we get the amount of pizza off by a whole slice, then we either overeat or leave utility on the table.
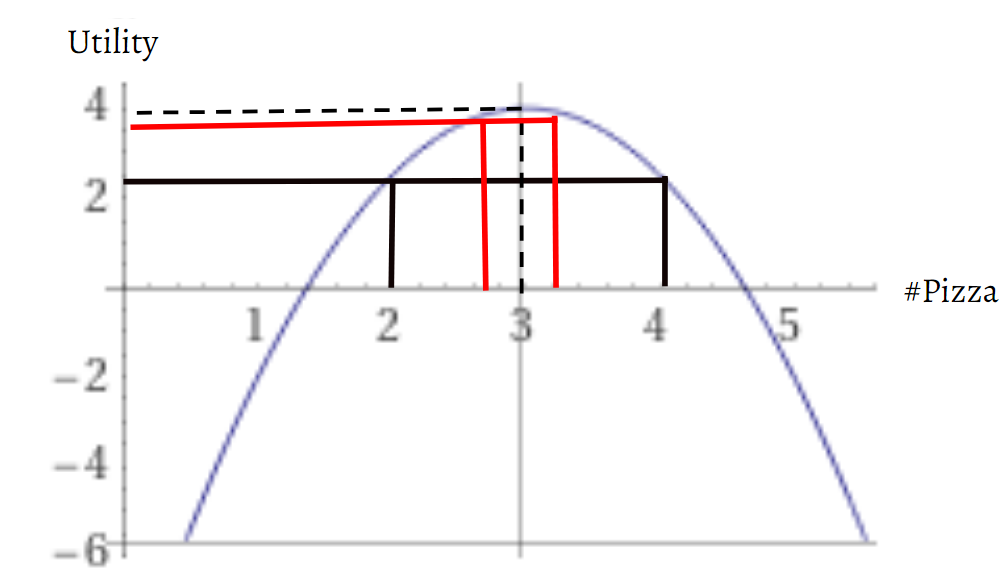
If we get it wrong by one bite, though, say a tenth of the pizza, we keep much closer to the optimum than the percentage we got wrong would suggest.
This corollary is that you should focus most of your energy on getting a problem approximately right, than don’t sweat the details. For example, during the bug hunt part of the character sheet class, a member of my cohort mentioned that she was having trouble maintaining personal hygiene because she found it too easy to get distracted by TV, podcasts, etc. instead of showering. As it happened, I’d solved this problem by getting a waterproof speaker. She did so and it’s worked well for her.
In a different context, I made a similar suggestion. Only there, the conversation devolved into a debate about which speaker was the best value proposition. All in all, the latter conversation took about double the energy from everyone involved as the former, and the improvement in utility for getting a slightly better speaker after realizing you should get one at all was certainly modest at best.
So, those are the rules for life which we can derive from unconstrained optimization. The next video will cover the same rules for constrained optimization, which is a far more generalized topic.